BFS(广度优先算法)

一、BFS是什么

先用百度百科的来讲：
BFS（又称广度优先搜索）是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和广度优先搜索类似的思想。属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。

简单来说，BFS是一种图搜索的算法，目的是用于搜索检查每一个可以达到的点,直到找到结果为止。他和DFS的区别：DFS是一条路走到黑，如果没用路就返回，而BFS是从上往下层次依序遍历，我们一般用队列来实现BFS的遍历。

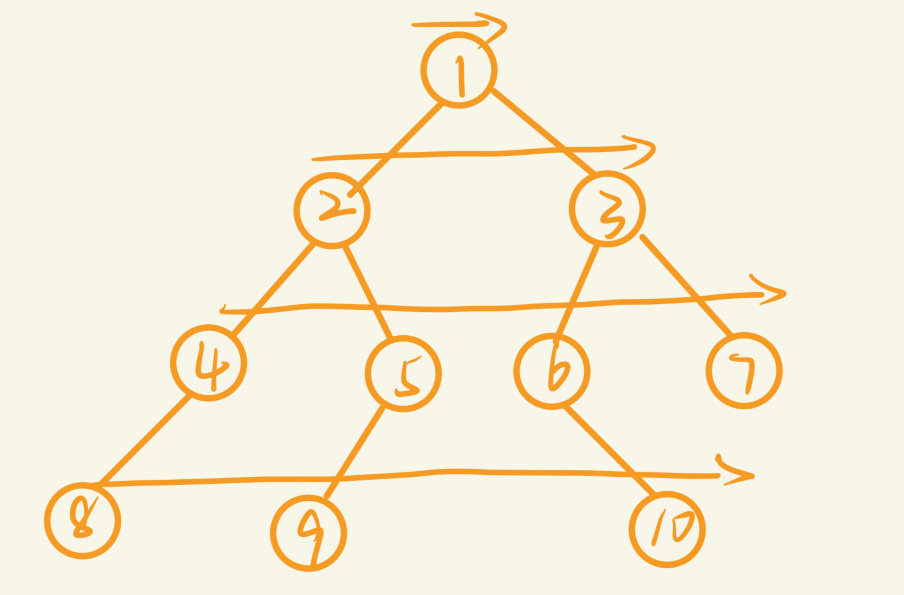
图解：（箭头的遍历方式）1 -> 2 -> 3 -> 4 -> 5 - > 6 -> 7 - > 8 - > 9 -> 10;

二、BFS的使用步骤

可以分为四个步骤：初始化（初始化队列和所求的值） -> 判空取队头（判断是否为空并取出队头） -> 拓展（利用队头去扩展） -> 判断入队（如果符合，将该点入队）。

void bfs(){
    queue<int>q;
    q.push(初始位置);

    //初始化
    while(q.size()){
        int t = q.front();
        q.pop();//取出队头的点，用该点向周围扩散。
        if(check(j)){       //如果该点可行就将它加入队列中
            q.psuh(j);      
            //实施相应的操作 
        }
    } 
} 

三、迷宫问题

迷宫问题：

完整代码:

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;
int n, m;
int g[N][N], d[N][N];
int dx[4] = {0, -1, 0, 1}, dy[4] = {1, 0, -1, 0};

void bfs(){
    // 初始化
    queue<PII> q;
    q.push({0, 0});
    memset(d, -1, sizeof(d));
    d[0][0] = 0;

    // 拓展
    while(q.size()){
        auto t = q.front();
        q.pop();
        int x = t.first, y = t.second;
        for (int i = 0; i < 4; i ++){
            int a = x + dx[i], b = y + dy[i];
            if (a >= 0 && a < n && b >= 0 && b < m && g[a][b] == 0 && d[a][b] == -1){
                d[a][b] = d[x][y] + 1;
                // 入队
                q.push({a, b});
            }
        }
    }
    cout << d[n - 1][m - 1] << endl;
}

int main(){
    cin >> n >> m;
    for (int i = 0; i < n; i ++){
        for (int j = 0; j < m; j ++){
            cin >> g[i][j];
        }
    }
    bfs();
    return 0;
}