DFS(深度优先算法)

一、DFS是什么？

DFS（深度优先搜索算法）：一种用于遍历或者树或者图的算法，是一种递归程序，不断递归达到无法在到达的点，简单点来说：一条路一直走，走到没有路后就原路返回，重新选择另一条 dfs(step + 1)。

DFS = 暴搜 + 回溯算法 + 剪枝（大多数是这样）。DFS需要回溯算法，其他算法也需要回溯算法，两种是一种调用关系。

暴搜：一条路走到黑（直接递归走到底）

回溯：DFS 开启另一条路则需要回溯，如果暴搜那条路找不到答案就要回溯走另外一条道路。

剪枝：如果明确接下来的搜索找不到答案或者不是最优解，就不再进行搜索并对路径进行回溯，从而达到减少问题搜索规模的目的。

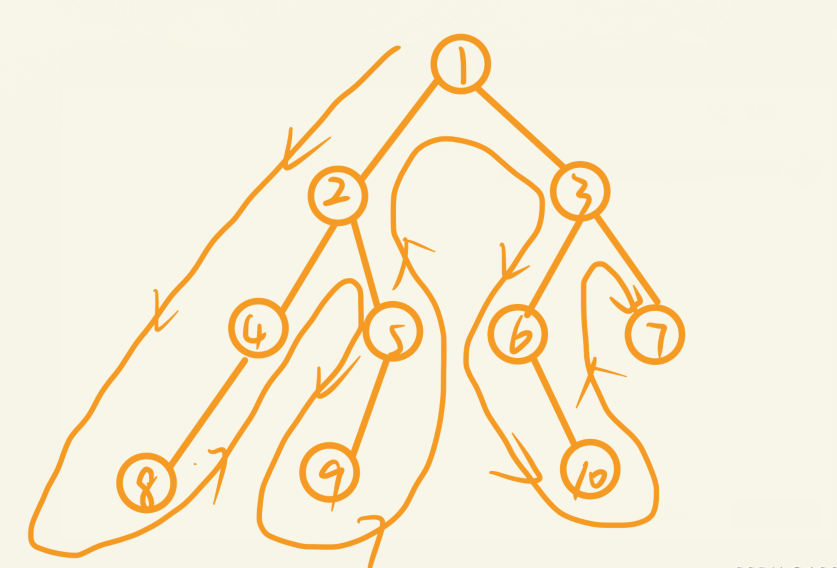
图解：（箭头的遍历方式）1 -> 2 -> 4 -> 8 -> 4 -> 2 -> 5 -> 9 - > 5 -> 2 -> 1 -> 3 -> 6 -> 10

-> 6 -> 3 -> 7。

二、DFS的使用步骤

void dfs(int step){ //step搜索的路径步骤
    判断边界问题{
        进行操作（如搜索完，并找到答案）
    }
    尝试每一种可以走的路径{
        check() return ;//剪枝
        标记该状态已经走到
        继续下一步搜索 DFS(step + 1)
        回溯（回到最开始的状态）
    }
}

三、N皇后问题

n皇后问题：

解决代码：

#include <iostream>
using namespace std;
const int N = 10;
bool col[N], row[N], dg[N], udg[N];
char g[N][N];
int n;

void dfs(int x, int y, int s){
    if (y == n){
        x ++;
        y = 0;
        if (x == n) {
            if (s == n){
                for (int i = 0; i < n; i ++) puts(g[i]);
            }
            return ;
        }
    }
    dfs(x, y + 1, s);

    if (!col[x] && !row[y] && !dg[x + y] && !udg[x - y + n]){
        col[x] = row[y] = dg[x + y] = udg[x - y + n] = true;
        g[x][y] = 'Q';
        dfs(x, y + 1, s + 1);
        g[x][y] = '.';
        col[x] = row[y] = dg[x + y] = udg[x - y + n] = false;
    }
}

int main(){
    cin >> n;
    for (int i = 0; i < n; i ++){
        for(int j = 0; j < n; j ++){
            g[i][j] = '.';
        }
    }
    dfs(0, 0, 0);
    return 0;
}