邻接表和邻接矩阵、树的遍历

一、邻接表与邻接矩阵

1.1 稠密图与稀疏图

图的储存方式分两种：邻接表和邻接矩阵。 了解邻接矩阵和邻接表之前我们要先学会稠密图、稀疏图。

百度百科来说：稠密图、稀疏图。

稀疏图：有很少条边或弧（边的条数|E|远小于|V|²）的图称为稀疏图（sparse graph）。

稠密图：有很多条边或弧 (边的条数|E|接近|V|²) 的图称为稠密图（dense graph）。

简单来说：我们假设某个图的点的个数 为 N, 边的个数为 M， 当 M << N ^ 2 (平方)（当边数远小于点的平方）时称为 稀疏图，当 M ≈ N ^ 2 （当边数约等于点的平方）时称为 稠密图， 如果图为稀疏图的时候，我们一般用邻接表储存，稠密图的时候，一般用邻接矩阵存储。

2.邻接矩阵的存储方式

邻接矩阵：邻接矩阵的储存方式是用一个二维数组g[a][b](a -> b的权值)来表示图的边的信息，a, b都是点， g[a][b] 表示a到b的距离。

图解：（图片来源于百度百科）

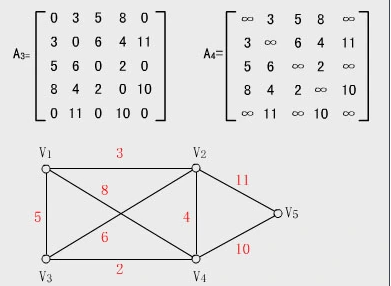
代码：

//运用在最短路或者最小生成树中邻接矩阵的代码方式
while(m --){ //m条边 
    int a, b, w;
    cin >> a >> b >> w;
    g[a][b] = min(g[a][b], w); //取最小的边
}

1.3 邻接表的存储方式

邻接表：邻接表的储存方式是用单链表来存储，在单链表中，头结点存储的是a, 链表存储的可能是b, c , d。例如：a -> b -> c -> d表示a能到b、a能到c、a能到d。

链表结构有ne[ ]数组：next指针，e[ ]: a能到的点， w[ ]： a到b的距离。

图解：（图片来源于百度百科）

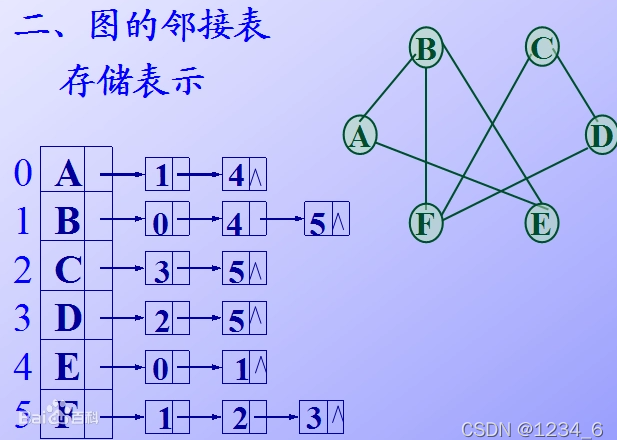
代码：

//idx 表示当前节点 
void add(int a, int b, int c){
    e[idx] = b; 
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx ++;
}

while(m --){ //m表示边数 
    int a, b, c;
    cin >> a >> b >> c;
    add(a, b, c);
} 

二、树的遍历

2.1 DFS

代码：

void dfs(int u){
    st[u] = true;//已经遍历到了
    for(int i = h[u]; i != -1; i = ne[i]){ //遍历链表
        int j = e[i];
        if(!st[j]){
            dfs(j); //递归
            //进行相应的操作
        }
    }
}

2.2 BFS

代码：

int bfs(){
    queue<int>q;
    q.push(1);
    while(q.size()){
        int t = q.front();
        q.pop();
        for(int i = h[t]; i != -1; i = ne[i]){ //遍历链表
            int j = e[i];
            q.push(j); //入队
        }
    }
}