最小生成树 (Prim算法和Kruskal算法)

一、最小生成树什么？

1.1 定义

最小生成树： 一个有n个结点的连通图的生成树是原图的最小连通图，且包含原图的所有n个结点，并且保持图的连通的最少的边。

最小生成树可以用：Prim算法和kruskal算法求出

1.2 应用

1. 铺设电缆： 以尽可能低的总价去铺设城市之间的电缆（假设每两个城市可以连通）

2. 旅行家： 某人自驾游想花费最短的路程去旅行到自己所想去的城市（城市有n个 n > 2）

3. 连接道路： 与铺设电缆类似，以最小连通去连接每一个城市

1.3 性质

假设设G=(V，E）是一个连通网络，U是顶点集V的一个非空真子集。若(u，v）是G中一条“一个端点在U中（例如：u∈U），另一个端点不在U中的边（例如：v∈V-U），且（u，v）具有最小权值，则一定存在G的一棵最小生成树包括此边（u，v）
转载： 百度百科

二、Prim算法

思想： 采用了贪心的思想，与dijkstra算法有高度的相似性，对于包含 N 个顶点的连通网，每次从连通网中找出一个离集合S权值最小的点，通过不断加点到集合S中并加上其权值，然后更新点到集合S的距离来构建最小生成树， 别名又称加点法
时间复杂度： O（n ^ 2）
图解：dist[N]: 表示点到集合S的最短距离， st[N]:表示集合S（与Dijkstra类似）

• 将图上的点分为两个集合：分别是S集合和N集合
• S集合表示访问过的点（用st数组存储）
• N：表示未访问过的点

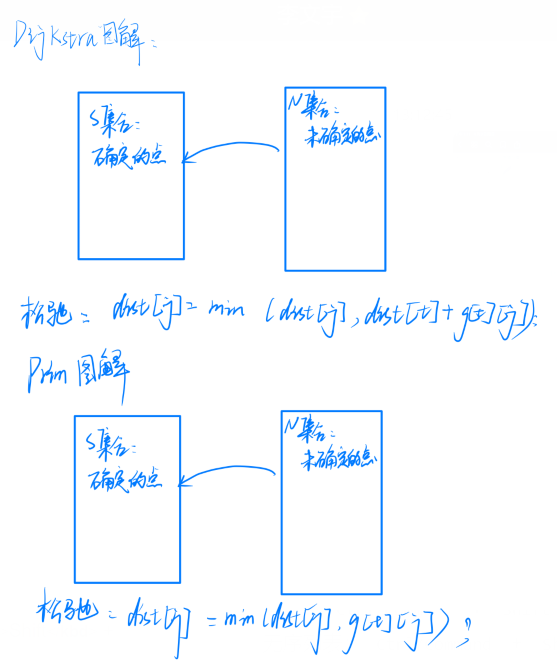
步骤：

• 与dijkstra算法不同的是dijkstra算法是更新集合N的点到起始点的距离，而prim算法是更新集合N的点到集合S的距离

1. 初始化距离： 把每个点到集合S的距离都初始化为正无穷（0x3f3f3f3f）

2. 加点： 进行n次循环，每循环一次就将集合N中离集合S最近的点t加入到集合S中 (st[t] = true)

3. 松弛操作： 用找到的点t去更新集合N到集合S的距离

   代码 + 注释：

const int N = 1e5 + 10;
int dist[N]; //点到集合S的距离 
int g[N][N]; //邻接矩阵 
bool st[N]; //是否加入到集合S中 
int prim(){
    memset(dist,0x3f3f3f3f ,sizeof dist);
    int res = 0;
    for(int i = 0; i < n; i ++){ //进行n次循环，每次循环加一个点 
        int t = -1;
        for(int j = 1; j <= n; j ++){
            if(!st[j] && (t == -1 || dist[t] > dist[j])) t = j;  //找点 
        }
        if(i && dist[t] == 0x3f3f3f3f) return 0x3f3f3f3f;//如果找到的点距离为无穷大，说明没有最小生成树 
        if(i) res += dist[t];   //加上权值 
        st[t] = true;           //加点 
        for(int j = 1; j <= n; j ++){        //松弛操作 
            dist[j] = min(dist[j], g[t][j]);
        }
    }
    return res;
}

三、kruskal算法

思想：kruskal算法(克鲁斯卡尔算法） 与Prim算法一样也是基于贪心思想而来的。但与Prim算法加点不同的是kruskal算法是通过加边来实现最小生成树的，对每条边的权值进行排序，然后根据权值由小变大依次来判断边的两个顶点是否属于同一个连通块，并用并查集的方法把边加入到同一个连通块中
时间复杂度：O（mlog2m） m表示边的数量 ==注意：结构体存储==
步骤：**

1. 排序： 对所有的边进行由小到大排序，然后依次进行遍历
2. 合并加边： 判断该边的两个顶点是否为同一个连通块，若是则合并两个顶点，并加入权值

代码 + 注释：

const int N = 2e5 + 10, INF = 0x3f3f3f3f;//N表示多少个点
int n, m;
int bin[N]; //祖宗结点

struct Edge{        //结构体存储
    int a, b, w;    //表示a -> b 的权值为w
    bool operator < (const Edge &W) const{
        w < W.w;
    }
}edges[N];

int find(int x){
    if(bin[x] != x) bin[x] = find(bin[x]);
    return bin[x];
}

int kruskal(){
    sort(edges, edges + m); //排序
    for(int i = 1; i <= n; i ++) bin[i] = i;
    int res = 0, cnt = 0;

    for(int i = 0; i < n; i ++){
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a), b = find(b);
        if(a != b){ //合并
            bin[a] = b;
            cnt ++; //有多少条边
            res += w; //加权值
        }
    }
    if(cnt < n -1) return INF;//如果边小于n - 1说明有点没有连接 
    else return res;
}