堆（手写堆包含STL）

一、堆的定义：

堆是什么，堆就像是一个金字塔，最顶端的是最值（最大值和最小值），堆其实就是一个二叉树，将最值元素放到根节点。子节点要么都小于父节点，要么都大于父节点。但是写手堆的话，我们用的是数组来存储，所以堆通常也被看做一颗树的数组对象。

二、堆的分类及性质

2.1 堆的分类：

大根堆和小根堆，根节点最大的堆叫大根堆，根节点最小的堆叫小根堆。

2.2 STL的定义：

首先要调用堆的头文件: #include

priority_queueheap;//默认的是大根堆

priority_queue<int, vector, greater>heap；小根堆

堆的函数：

• size();//堆的大小

• empty();//堆是否为空

• push();//插入一个元素

• top();//返回栈顶元素

• pop();//删除一个元素

3.3 堆的性质：

• 堆是一颗完全二叉树，只不过用数组实现。
• 堆中的数据不是完全有序的，它只是每个子节点的值大于或小于父节点的值

三、手写堆（重点）

3.1 手写堆的思想：

我们用数组的思想来存储堆，总共分为三个函数模块，五个操作模块。（模拟小根堆）

• 函数模块：

  1. h_swap()；//交换节点的位置和值

  2. up()；//将节点值与父节点比较往上移

  3. down；//将节点值与子节点比较往下移

• 操作模块：size:堆的大小，k:堆的第k个值（后面两个操作STL是不能实现的）

  1. 插入一个数值:heap[size ++] = x; up(size);
  2. 删除最小值：heap[1] = heap[size]; size --;down(1);
  3. 求集合中的最小值：heap[1];
  4. 删除任意第k个值: heap[k] = heap[size]; size --; down(k); up(k);
  5. 修改任意第k个值：heap[k] = x;down(k);up(k);

3.2 函数模块代码：

h_swap():交换节点（有点难懂）

void h_swap(int a, int b){
    swap(ph[hp[a]],ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
} 

理解 + 图解：这里是一种映射关系，p表示外部指针，h表示堆的位置（也可以理解为内部指针）

1. ph[ ]：表示外部指针指向内部指针
2. hp[ ]：表示内部指针指向外部指针
3. h[ ]：表示存放的数值

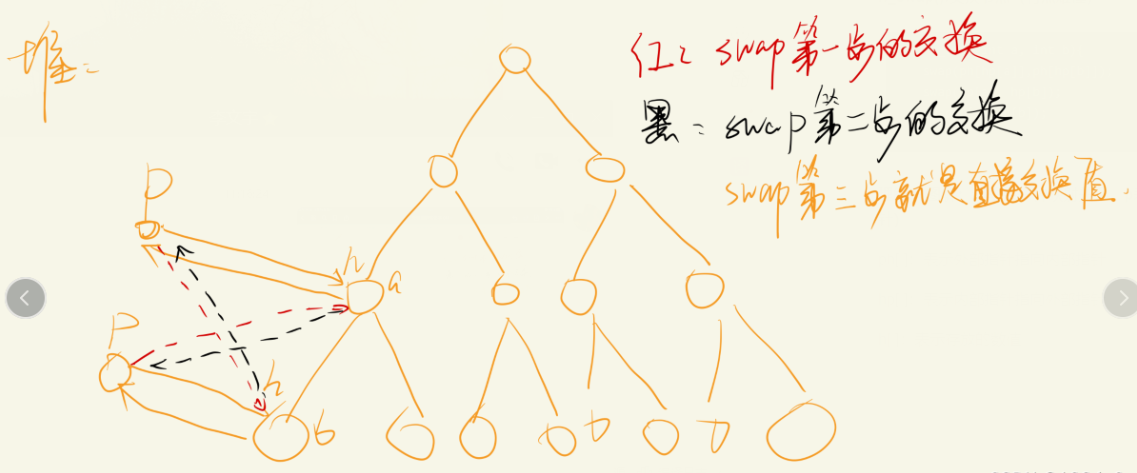
up();//节点上移操作：

void up(int u){
    if(u / 2 && h[u / 2] > h[u]){//如果小于根节点，就与根节点置换
        swap(u, u / 2);
        up(u / 2);
    }
}

down();//节点下移操作：

void down(int u){
    int t = u;
    if(u * 2 <= size && h[u * 2] < h[t]) t = u * 2;//比较左子树
    if(u * 2 + 1 <= size && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//比较右子树
    if(u != t){//若左子树或者右子树小于根节点就置换
        h_swap(u, t);
        down(t);//不断执行down()
    }
}

3.3 操作模块：

• 插入一个值：直接在数组尾部插入并up(szie)（队尾位置）
• 求集合中最小值：直接返回头部值
• 删除最小值：
  1. 这里要涉及一个知识点：为什么要在将头部值和尾部值交换
  2. 如果我们直接删除头部位置，那么所有的位置都会受到影响，所有置换一下，再删除尾部值，就其他位置就不会收到影响
  3. 最后我们再up(1), down(1);将头部值放到合适位置
• 删除第k个元素：与删除最小值是一样的，需要置换尾部位置和第k个值的位置
• 修改第k个元素：直接将heap[k] = x，再将x值放到合适位置

四、完整代码 + 注释

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int hp[N], ph[N], h[N], cnt, m;    //m表示ph的映射值，cnt表示大小size
int n;
void h_swap(int a, int b){
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

void down(int u){
    int t = u;
    if(u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if(u * 2 + 1<= cnt && h[u * 2 + 1]< h[t]) t = u * 2 + 1;
    if(u != t){
        h_swap(u, t);
        down(t);
    }
}
void up(int u){
    if(u / 2 && h[u / 2] > h[u]){
        h_swap(u / 2, u);
        up(u / 2);
    }
}

int main()
{
    cin >> n;
    while(n --){
        string op;
        int k, x;
        cin >> op;
        //插入操作
        if(op == "I"){
            cin >> x;
            cnt ++ ;
            m ++ ;
            ph[m] = cnt, hp[cnt] = m;
            h[cnt] = x;
            up(cnt);
        }
        //返回最小值
        else if(op == "PM") cout << h[1] << endl;
        //删除头部元素
        else if(op == "DM") {
            h_swap(1, cnt);
            cnt --;
            down(1);
        }
        //删除第K个节点
        else if(op == "D"){
            cin >> k;
            k = ph[k];
            h_swap(cnt, k);
            cnt --;
            up(k);
            down(k);
        }
        //修改第k个数
        else {
            cin >> k >> x;
            k = ph[k];
            h[k] = x;
            up(k);
            down(k);
        }
    }
    return 0;
}