浮点数的精度问题

lwy
Unity
2024-06-23
758热度
0评论

每个人在写关于浮点数判断大小的时候都会看到a - b < 1e8来确定a和b的数值是否相等，为什么不能适用a == b来直接判断呢？这个就涉及到了浮点数的精度问题。

下面一段代码

#include<iostream>
using namespace std;
int main(){
    float a = 0.1;
    float sum = 0;
    for (int i = 0; i < 3; i ++){
        sum = a + sum;
    }
    printf ("%0.8f", sum);
    return 0;
}

// 输出的值为0.30000001

最后输出的值为0.30000001,因为在浮点型的数据做运算的时候，得到的数据都不会精确。

一、浮点数的二进制存储方法

IEEE二进制浮点数算术标准中，单精度float类型使用32比特存储(32位占4字节)，其中1位为表符号，8位表示指数，23位表示尾数；双精度double类型使用64比特存储(64位占8字节)，1位符号位，11位指数位，52位尾数位。

计算机只能识别0和1，所以在浮点数中，不管是整数还是小数，在计算机中都以二进制方式来存储在内存中，其中整数部分采用"除以2取余法"从十进制数转换成二进制，而小数部分则使用"乘2取整法"得到二进制数。以120.5为例，9.625(10)中整数表示1111000,而小数表示1,即1.1110001×2^6。

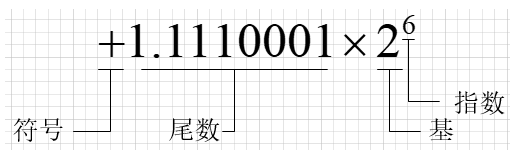
浮点数的存储一共分为三个部分:

符号位(sign):0表示正数，1表示负数。
指数位(exponent):存储科学计数法的指数部分。
尾数部分(fraction):表示科学技术法的尾数部分。

任何一个浮点数可以这样表示

F = （-1 ^ s) × (1.M) × (2 ^ e)

符号位即为s,尾数部位即为M,指数部位为e。

由此可以得出，结论二进制小数的科学计数法表示上看，可以知道float的精度为 1 / (2 ^ 23)，double的精度为1 / (2 ^ 52) 。

二、精度丢失

浮点数9.625可以用2进制表示为1.1110001×2^6，0.625可以精确的表示成101,那如果以198903.19为例，0.19则表示0011000010100011...,它转换为二进制是无穷尽的。而198903二进制为110000100011110111，那么表示二进制则为(-1^0)×1.100 001 000 111 101 110 011 000 010 100 011×(2^17)。在计算中存储时就会溢出，从而丢失精度。

在实际开发中我们遇到常见的精度问题:

数值比较不相等:

比如在Unity的Update函数中，如果我们需要设计一个在0.25秒执行某个逻辑，然后在0.65秒在做另外一个逻辑时，如果我们使用==那么就会遇到在0.25秒或者0.65秒并不会执行逻辑。我们只能用>或者<来解决该问题的出现。或者使用abs(X - 0.25) < 0.000001来判断x == 0.25。
不同设备的计算结果不同：

不同平台上的浮点数计算也有误差，由于设备上CPU存储器和操作系统架构不同，因此会导致相同的公式在不同的设备上计算出的结果有所差异。

三、精度丢失的解决办法

使用int或long来代替浮点数:浮点数和整数的计算方式是一样的，小数点部分会造成精度问题，不如通过将浮点数乘10的次幂来得到整数，在用整数进行运算，根据需要的精度用整数表示，如保留3位精度就乘以10000。
用定点数保持一致性：定点数是把整数部分和小数部分拆分开来，都以整数的形式表示，这样计算和表示都是用整数的方式，就不会产生误差，C#有一种decimal的128位的数据类型，用于表示高精度的实数，其内部就是定点数的实现方式(注意:decimal不能与float随意互换)，也可以自己实现一个定点数逻辑。
用字符串代替浮点数:在学校写算法题时基本上都会遇到过字符串来解决上百位的数字的高精度运算，字符串形式存储数字，这样的计算方式不用担心越界问题，但是CPU和内存的消耗比较大，只能做少量高精度的计算。